数字电路是数字IC设计的基础,而数制和码制往往又是数字电路的基础,因此数制和码制是数字IC设计基础的基础。在这里,我将记录关于数制与码制的一些主要知识点,有些知识点我是学了数电半年或者一年之后才发现,原来数电还有这样子的东西,于是整理在这里,仅供参考,有误请评论指出。
一、数制
这里不进行记录什么二进制、十进制之类的基本概念,只介绍一些主要的知识点。
1、数制之间的转换
(1)关于二进制的一些概念
这里主要记录一下位、比特对于二进制的描述,是比较基础的东西。
位宽/比特:一个二进制数,有它的位宽,有多少个0/1,它位宽就是多少;比如二进制数10110,它的位宽就是5,从第0位到第4位;也说这是一个5位宽的二进制数,或者说这个二进制数宽度大小是5比特,数值大小为22(默认数值大小一般说的是十进制的数值大小)。
最高位和最低位:对于上面的10110,最高位是1,最低位是0;最高位是第4位,最低位是0
(2)二进制转换成十进制:
①二进制转换成十进制方法为:把二进制数按权展开、相加即得十进制数。
②举例:二进制数10011.01,位数为1的有第4位,第1位,第0位,第-2位,那么就有:
10011的十进制数值(注意说到数值,默认是转换为十进制时数的大小)为:2^4 + 2^1 + 2^0 + 2^(-2) = 19.25
十进制转换成二进制:
①转换方法就是:整数部分,除二取余;小数部分,乘二取整(小数部分一般会说明要精确到小数点多少位)。
②举例说明:将35.63转换成二进制数,小数部分精确到小数点后3位
那么对于整数部分,除二取余:
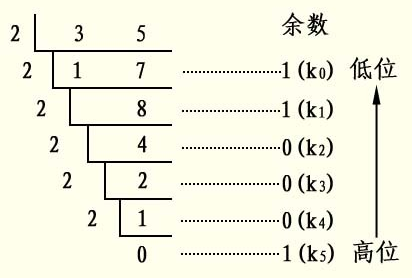
整数部分的二进制数就是100011。
对于小数部分:乘二取整
0.63*2 = 1.26,取1;0.26*2 = 0.52,取0;0.52*2 = 1.04,取1;已经达到三位了。因此小数部分就是101
因此35.63的二进制表示为100011.101。
(3)二进制转换成八进制:
①方法:从小数点向两边展开,每三位二进制划分为一组,每一组的的十进制就是对应的八进制,(注意,最高位或者最低位不够3位要补0)。
②举例:1001.01转换成八进制,进行分组 (00)1 001 . 01(0),转换成八进制就是11.2。
八进制转换成二进制:
①八进制转换成二进制的方法跟二进制转换成八进制的方法相反,一位八进制对应三位的二进制,依次展开就可以。
②举例:八进制67.21转换成二进制,6是110,7是111,2是010,1是001;所以对应的二进制就是110111.010001。
(4)二进制转换成十六进制,十六进制转换成二进制:
二进制转换成十六进制/十六进制转换成二进制与八进制的类似,只不过是八进制对应的是3位,而十六进制对应的是4位;这里不再详述。
它们之间的转换都可以通过二进制进行。
2、二进制的有符号与无符号
(1)无符号数,也就是没有正负之分,默认为正值,上面说到的都是正数,也就是无符号数。对于二进制也是这样。
·一般情况下,没有专门指出这个数是有符号的,就默认是无符号的数。
·n位无符号可以表示的范围位0~+(2^n-1),即0~1...1
(2)有符号数,顾名思义就是有正负之分,比如+39,-49。对于二进制数而言,也有有符号数之分。以后我记录的说到有符号数的,默认指有符号数的二进制数。
①在有符号的二进制数中,最高位表示符号位,其他位表示数的其他内容;其中符号位是1时,表示这个有符号的二进制数是负数;符号位是0时,表示这个有符号的二进制数是正数。
比如有符号数10010,最高位是1,表示这个二进制数是负数。
·从前面上述可以知道,一个有符号的二进制数,至少有两位,其中一位是符号位。
②有符号二进制数有三种表达方式:原码、反码、补码(十进制之类的也有补码之类的,这里仅仅记录与二进制有关的)。
③原码:符号位+剩余二进制表示。最高位是符号位,除最高位后的二进制数,表示二进制数值的绝对值大小。
比如原码100110,最高位是1,表示负数;剩余是00110,表示的数值大小是6,那么这个原码表示的数值大小就是-6 。
·一般情况下,说到是有符号数,一般指的是原码。
·原码的0,可以表示为+0和-0,也就是1...0,0..0,因此有两种表达形式。
·n位原码表示的范围为:-(2^(n-1)-1)~+(2^(n-1)-1),即1...1~0...1
④反码:符号位+剩余二进制表示。最高位也是符号位,除符号位的二进制数值与符号位有关,符号位是0,表示这个编码的是正数,除符号位剩下的就表示数值绝对值大小。若符号位是1,则除符号位剩下位数取反后,表示的才是数值绝对值大小。
比如一个有符号数的反码是10011,则有:首位是1,表示这个是负数,剩余位是0011,取反后是1100,所以绝对值大小是12,因此10011是十进制数-12的反码表示。
·反码在应用不多,也许是我还没有了解到吧,在此不详述,以后用到了再详述记录吧。
⑤补码:符号位+剩余二进制表示。补码的应用就广泛了,计算机的内部运算就是用补码的。
补码也可以由原码得来:
对于正数:二进制数值的绝对值即为补码;
对于负数:原码的符号位不变,剩余位取反,然后整体加一就得到了补码。
比如:二进制的原码是10010,符号位1不变;剩余0010,取反得1101;整合为11101,加一得到11110.也就是原码是10010的补码为11110 。
·补码的0,假设有4位,那么对于-0,原码是1000,进行取反加一后,得到0000(假设位宽固定);对于+0,补码也是0000;因此补码的0只有一种表达形式。
·n位补码表示的数值范围为:-2^(n-1)~+(2^(n-1)-1)
3、二进制的加减运算与溢出现象
(1)二进制的加减运算
①对于一般的无符号运算,直接运算就好了,没什么可以说的。但是计算机内部,它是用补码运算的,这就有可以记录的地方了,补码的加减运算对于其他的有符号数,就显得比较简单了。此外,减法也可以当成加法来,减一个数可以当成加这个数的负数。
②对于补码的加法运算有:补码 + 补码 = 补码。当然这个是有一定的条件的,下面举例探讨。
③例一:(+3) + (+4),结果显然是+7;用二进制补码进行运算,则是0011+0100,得到的结果是0111,很显然,0111是+7的补码。
例二:(-2) -6 = (-2)+ (-6),结果显然是-8;用二进制补码进行运算,则是1110 + 1010 ,得到11000,这个很显然也是-8的补码。
例三:+6 - 3 = (+6)+ (-3),结果显然是+3;用二进制补码进行运算,则是0110+1101,结果是10011,诶呀,这个很显然就不是+3的补码,但是,当我们去掉最高位后,只看低四位0011,这个很显然是+3的补码呀。
例四:+4-7 = (+4)+(-7),结果是显然是-3;用二进制补码进行运算,则是0100+1001,得到的结果是1101,这个结果很显然是-3的补码。
(2)溢出现象
①经过上面的四个例子,引入溢出这个概念:如果加法操作产生的几个超出了数制定义的范围,就说发生了溢出。两个异号数相加,肯定不会溢出;同号相加可能溢出。
②判断溢出的法则:如果加数的符号相同,而和的符号与加数符号不同,则有加法溢出。
③再谈前面的四个例子:
一般而言,对于位宽固定的情况下,
例一相加,得到的是4位,没有溢出,结果也正确。
例二,虽然得到的结果正确,但是得到的结果是5位的,如果截去最高位,那么得到结果将是错误的,也就是有溢出产生。这里也提醒我们,对于同号相加,要加多一位,其实也就是加多一个进位位。
例三结果虽然是不正确的,但是这是5位的结果,我们截去最高位,这个结果是对的,因此这个没有溢出,也就是这个结果(四位)还是对的。
例四,没有溢出。
二、编码
第二篇记录一下编码。
编码:用于表示不同的数或其他事件的一组n位二进制码的集合,称为一种编码。
码字:一个含义确切的特定的n位组合,称为码字。
总之可以这么理解,编码就是一种表达二进制数集合的方式。
1、十进制数的二进制编码
①十进制数的二进制编码也就是用二进制表示10个十进制数0~9 。
②十进制数的二进制编码方式主要有:BCD码,也叫8421码;5421码;2421码;余3码。下面是表格,但是这里值简述一下8421码;2421码;余3码。
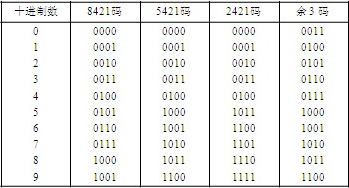
③8421码:如上图所示,是最习惯用二进制表示十进制数的一种方式。最高位的值是8,次高位是4,次低位是2,最低位是1 。因此一个二进制数1001表示的数值就是1*8+1*1 = 9 。也就是按权展开就是十进制数值了。
④2421码:数值小于等于4时,2421码等于8421码;数值大于4时等于8421码加6 。
⑤余3码:8421码加上0011就对应数值的余3码。
2、格雷码
(1)概念:百度百科是这样说的:在一组二进制数的编码中,若任意两个相邻的二进制数只有一位二进制数不同,则称这种编码为格雷码。
·由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。
(2)二进制与格雷码的相互转换:这里的二进制不是只BCD码,就是自然的二进制。
①二进制转换为格雷码:
转换方法:
自然二进制的最高位与格雷码的最高位相同;然后从最低边一位起,依次将每一位与左边一位进行比较,相同取0,不同取1,(也就是异或运算)作为对应格雷码该位的值。
举例比较方便:
110010转换成格雷码:
过程图:
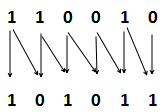
首先最高位是1,那么格雷码最高位是1;然后从最低位起跟左边一位进行比较;
最低位是0,它的左边一位是1,因此得到格雷码的最低位是1;
次低位是1,它的左边一位是0,因此得到次低位的格雷码是1;
次次低位0,它的左边一位是0,因此得到次次低位的格雷码是0;
...
次高位是1,它的左边一位是1(也就是最高位),因此格雷码的次高位是0;
这样就得到格雷码:101011 。
②格雷码转二进制码:
转换方法:
这个转换方类似,只不过是倒着回来;同样保留格雷码的最高位作为自然二进制码的最高位,而次高位自然二进制码为最高位自然二进制码与次高位格雷码相异或(就是那个相同取0,不同取1),而自然二进制码的其余各位与次高位自然二进制码的求法相类似。
举例吧:
把格雷码101101转换成二进制数:
过程图:
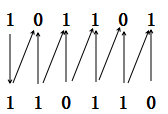
转换过程不再详述。
(3)格雷码的特点:
百度百科总结如下:
①格雷码属于可靠性编码,是一种错误最小化的编码方式。
·自然二进制码可以直接由数/模转换器转换成模拟信号,但在某些情况,例如从十进制的3转换为4时二进制码的每一位都要变,能使数字电路产生很大的尖峰电流脉冲。
·格雷码则没有这一缺点,它在相邻位间转换时,只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。
·由于格雷码相邻的两个码组之间只有一位不同,因而在用于方向的转角位移量-数字量的转换中,当方向的转角位移量发生微小变化(而可能引起数字量发生变化时,格雷码仅改变一位,这样与其它编码同时改变两位或多位的情况相比更为可靠,即可减少出错的可能性。
②格雷码是一种绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。
③格雷码是一种变权码,每一位码没有固定的大小,很难直接进行比较大小和算术运算,也不能直接转换成液位信号,要经过一次码变换,变成自然二进制码,再由上位机读取。
④典型格雷码是一种采用绝对编码方式的准权码,其权的绝对值为2^i-1(设最低位i=1)。
⑤格雷码的十进制数奇偶性与其码字中1的个数的奇偶性相同。
3、ASCII码
(1)简介
ASCII(American Standard Code for Information Interchange,美国信息交换标准代码)是基于拉丁字母的一套电脑编码系统,主要用于显示现代英语和其他西欧语言。它是现今最通用的单字节编码系统。
(2)一个ASCII码用8位二进制表示。
只记录这些,详情自己Google或者百度吧。
4、其他编码
其他的编码,如奇偶校验码、循环冗余检验码(CRC)、汉明码、二维码、NRZ编码、霍夫曼编码、曼彻斯特编码等等这些编码在以后应用到的时候,再进行记录。